
- #On each trial of a digit span memory task full#
- #On each trial of a digit span memory task software#
Note: trialnum is a built-in Inquisit variable it counts all trials run even those
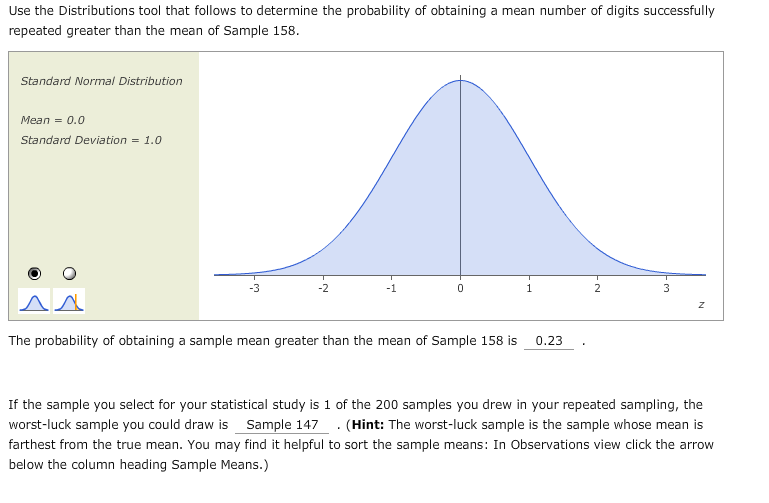
Trialcode, trialnum: the name and number of the currently recorded trial (built-in Inquisit variable) Subject, group: with the current subject/groupnumberīlockcode, blocknum: the name and number of the current block (built-in Inquisit variable) (1) Raw data file: 'digitspanvisual_forward_raw*.iqdat' (a separate file for each participant)īuild: The specific Inquisit version used (the 'build') that was runĬatform: the platform the script was run on (win/mac/ios/android) The default data stored in the data files are: The default set-up of the script takes appr. Participants see digit sequences and have to recall them in the order presentedīy selecting the digits from a circle of digits with the mouse.ĭepending on performance, participants move up a level or down a level. Journal of Clinicial and Experimental Neuropsychology, 33, 101-111 Improving digit span assessment of short-term The Two Error Maximal Lenght (TE_ML), which is the traditional digit span measure,Īnd a new measure MeanSpan (MS), the digit span that a participant is supposed to get correct 50% of the time. This script implements the Digit Span procedure, a measure of working memory, with two main measures
#On each trial of a digit span memory task software#
Script Copyright © 02-21-2022 Millisecond Software You may find it helpful to sort the sample means: In Observations view click the arrow below the column heading Sample Means.DIGIT SPAN (VISUAL) - Forward Assessment only Standard Normal Distribution Mean-00 Standard Deviation = 1.0 0 0 1 AA The probability of obtaining a sample mean greater than the mean of Sample 103 is If the sample you select for your statistical study is 1 of the 200 samples you drew in your repeated sampling, the worst-luck sample you could draw is (Hint: The worst-luck sample is the sample whose mean is farthest from the true mean. The Z-score corresponding to the mean of Sample 103 is Use the Distributions tool that follows to determine the probability of obtaining a mean number of digits successfully repeated greater than the mean of Sample 103. The mean for Sample 103 is for Sample 103 is Using the distribution of sample means, calculate the 2-score corresponding to the mean of Sample 103. The standard deviation Use the DataView tool to find the mean and the standard deviation for Sample 103. The samples are numbered in the first column, and you can use the scroll bar on the right side to scroll to the sample you want.). (Hint: To see a particular sample, click the Observations button on the left-hand side of the DataView tool. Suppose this professor happens to select Sample 103. Minimum Varia! Maximum Go Correlation Correlation
#On each trial of a digit span memory task full#
Data Set Samples Sample SD Variable Sample SD Location Full Data Quartiles Full Data Sample SD Minimum Median Mean Maximum 1.293 1.628 1.629 1.977 Q1 Median 03 Quantitative 1.555 1.628 1.701 Observations - 200 Missing = 0 Values - 200 Statistics Variability & Shape Values Range Interquartile Range Standard Deviation Coefficient of Variation Skewness 200 0.684 0.146 0.117 Deciles 10% 20% 30% 40% Median 60% 70% 80% 90% Histogram 1.483 1.536 1.570 1.603 1.628 1.655 1.687 1.723 1.772 0.02 Box Plots Filter: Include observations between.
(Hint: Use the population mean and/or standard deviation just The expected value of the mean of the 64 randomly selected students, M, is given to calculate the expected value of M.) The standard error of M Is (Hint: Use the population mean and/or standard deviation just given to calculate the standard error.) The DataView tool that follows displays a data set consisting of 200 potential samples (each sample has 64 observations). The professor knows that the distribution of scores is normal, but she does not know that the true average number of digits successfully repeated on the digit span task among college students is 7.06 digits with a standard deviation of 1.610 digits. She measures the number of digits successfully repeated for 64 randomly selected students. A professor of cognitive psychology is interested in the number of digits successfully repeated on the digit span task among college students. The participant's score is the longest string of digits she can successfully repeat. For instance, if the participant repeats four digits successfully, she will hear five random digits on the next trial. If the participant is successful, the length of the next string is increased by one. The participant must then repeat the digits in the correct order.

On each trial of a digit span memory task, the participant is asked to read aloud a string of random digits.


 0 kommentar(er)
0 kommentar(er)
